如图,在矩形 中, ,两条对角线相交于点 .以 为邻边作第 个平行四边形 ,对角线相交于点 ;再以 为邻边作第 个平行四边形 ,对角线相交于点 ;再以 为邻边作第 个平行四边形 ;…,依此类推.
(1)求矩形 的面积;
(2)求第 个平行四边形 、第 个平行四边形 和第 个平行四边形的面积.
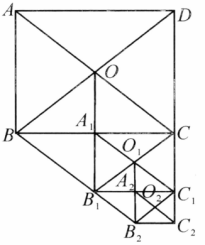
如图,在矩形 中, ,两条对角线相交于点 .以 为邻边作第 个平行四边形 ,对角线相交于点 ;再以 为邻边作第 个平行四边形 ,对角线相交于点 ;再以 为邻边作第 个平行四边形 ;…,依此类推.
(1)求矩形 的面积;
(2)求第 个平行四边形 、第 个平行四边形 和第 个平行四边形的面积.
