如图所示的方格纸( 格长为一个单位长度)中, 的顶点坐标分别为 .
(1)将 沿 轴向左平移 个单位,画出平移后的 (不写作法,但要标出顶点字母);
(2)将 绕点 顺时针旋转 ,画出旋转后的 (不写作法,但要标出顶点字母);
(3)在(2)的条件下,求点 绕点 旋转到点 所经过的路径长(结果保留 ).
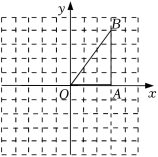
如图所示的方格纸( 格长为一个单位长度)中, 的顶点坐标分别为 .
(1)将 沿 轴向左平移 个单位,画出平移后的 (不写作法,但要标出顶点字母);
(2)将 绕点 顺时针旋转 ,画出旋转后的 (不写作法,但要标出顶点字母);
(3)在(2)的条件下,求点 绕点 旋转到点 所经过的路径长(结果保留 ).
