【问题提出】
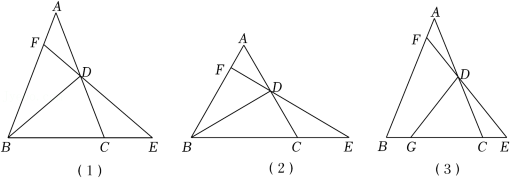
如图(1),在 中, , 是 的中点,延长 至点 ,使 ,延长 交 于点 ,探究 的值.
【问题探究】
(1)先将问题特殊化.如图(2),当 时,直接写出 的值;
(2)再探究一般情形.如图(1),证明(1)中的结论仍然成立.
【问题拓展】
如图(3),在 中, , 是 的中点, 是边 上一点, ,延长 至点 ,使 ,延长 交 于点 .直接写出 的值(用含 的式子表示).
【问题提出】
如图(1),在 中, , 是 的中点,延长 至点 ,使 ,延长 交 于点 ,探究 的值.
【问题探究】
(1)先将问题特殊化.如图(2),当 时,直接写出 的值;
(2)再探究一般情形.如图(1),证明(1)中的结论仍然成立.
【问题拓展】
如图(3),在 中, , 是 的中点, 是边 上一点, ,延长 至点 ,使 ,延长 交 于点 .直接写出 的值(用含 的式子表示).
