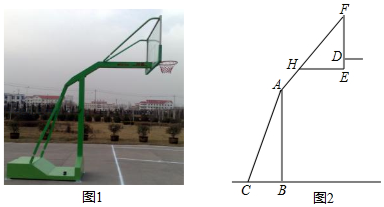
如图1,2分别是某款篮球架的实物图与示意图,已知底座 米,底座 与支架 所成的角 ,支架 的长为2.50米,篮板顶端 点到篮筐 的距离 米,篮板底部支架 与支架 所成的角 ,求篮筐 到地面的距离(精确到0.01米)(参考数据: , , , ,
相关知识点
推荐套卷
如图1,2分别是某款篮球架的实物图与示意图,已知底座 米,底座 与支架 所成的角 ,支架 的长为2.50米,篮板顶端 点到篮筐 的距离 米,篮板底部支架 与支架 所成的角 ,求篮筐 到地面的距离(精确到0.01米)(参考数据: , , , ,
