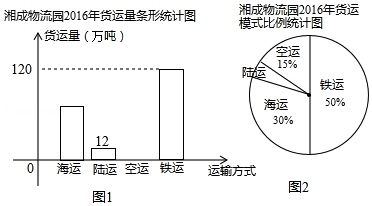
在“一带一路”倡议下,我国已成为设施联通,贸易畅通的促进者,同时也带动了我国与沿线国家的货物交换的增速发展,如图是湘成物流园2016年通过“海、陆(汽车)、空、铁”四种模式运输货物的统计图.
请根据统计图解决下面的问题:
(1)该物流园2016年货运总量是多少万吨?
(2)该物流园2016年空运货物的总量是多少万吨?并补全条形统计图;
(3)求条形统计图中陆运货物量对应的扇形圆心角的度数.
推荐套卷
在“一带一路”倡议下,我国已成为设施联通,贸易畅通的促进者,同时也带动了我国与沿线国家的货物交换的增速发展,如图是湘成物流园2016年通过“海、陆(汽车)、空、铁”四种模式运输货物的统计图.
请根据统计图解决下面的问题:
(1)该物流园2016年货运总量是多少万吨?
(2)该物流园2016年空运货物的总量是多少万吨?并补全条形统计图;
(3)求条形统计图中陆运货物量对应的扇形圆心角的度数.
