为抗击疫情，支持武汉，某物流公司的快递车和货车每天往返于物流公司、武汉两地，快递车比货车多往返一趟，如图表示两车离物流公司的距离 （单位：千米）与快递车所用时间 （单位：时）的函数图象，已知货车比快递车早 小时出发，到达武汉后用 小时装卸货物，按原速、原路返回，货车比快递车最后一次返回物流公司晚 小时．
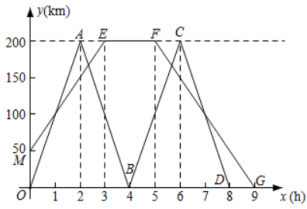
（ 1 ）求 的函数解析式；
（ 2 ）求快递车第二次往返过程中，与货车相遇的时间．
（ 3 ）求两车最后一次相遇时离武汉的距离．（直接写出答案）
相关试题
下表中，y是x的一次函数．
| x |
 2 |
1 |
2 |
5 |
|
| y |
6 |
3 |
12 |
15 |
（1）求该函数的表达式，并补全表格；
（2）已知该函数图象上一点M（1，-3）也在反比例函数
图象上，求这两个函数图象的另一交点N的坐标．
．如图，在平面直角坐标系中，已知矩形AOBC的顶点C的坐标是（2，4），动点P从点A出发，沿线段AO向终点O运动，同时动点Q从点B出发，沿线段BC向终点C运动．点P、Q的运动速度均为1个单位，运动时间为t秒．过点P作PE⊥AO交AB于点E．
（1）求直线AB的解析式；
（2）设△PEQ的面积为S，求S与t时间的函数关系，并指出自变量t的取值范围；
（3）在动点P、Q运动的过程中，点H是矩形AOBC内（包括边界）一点，且以B、Q、E、H为顶点的四边形是菱形，直接写出t值和与其对应的点H的坐标．
PC．（不必证明）
粤公网安备 44130202000953号