如下图，已知正方体 的棱长为２，点Ｅ是正方形 的中心，点Ｆ、Ｇ分别是棱 的中点．设点 分别是点Ｅ，Ｇ在平面 内的正投影．
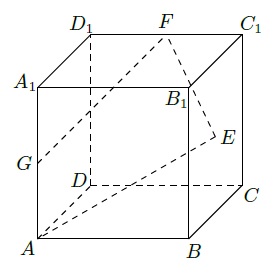
（１）求以Ｅ为顶点，以四边形 在平面 内的正投影为底面边界的棱锥的体积；
（２）证明：直线 ；
（３）求异面直线 所成角的正弦值.
相关试题
}的前n项和为
，已知
成等差数列．
}的公比q；
＝3，求
,
,
，且
，
，
两两的夹角都是
，
； 
；
与
中, 
求
的值
满足：
，其中
为数列
项和.（Ⅰ）试求
Ⅱ）若数列
满足：
，试求
项和公式
；（III）设
，数列
的前
，求证：
．
的前
项和为
，对任意
，点
都在函数
的图像上．
，
是数列
的前
对所有
．推荐套卷
如下图，已知正方体 的棱长为２，点Ｅ是正方形 的中心，点Ｆ、Ｇ分别是棱 的中点．设点 分别是点Ｅ，Ｇ在平面 内的正投影．
（１）求以Ｅ为顶点，以四边形 在平面 内的正投影为底面边界的棱锥的体积；
（２）证明：直线 ；
（３）求异面直线 所成角的正弦值.
粤公网安备 44130202000953号