如图所示,等腰△ABC的底边AB=6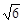 ,高CD=3,点E是线段BD上异于点B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.记
,高CD=3,点E是线段BD上异于点B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.记 ,用
,用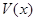 表示四棱锥P-ACFE的体积.
表示四棱锥P-ACFE的体积.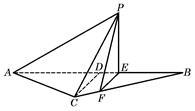
(Ⅰ)求 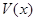 的表达式;
的表达式;
(Ⅱ)当x为何值时,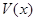 取得最大值?
取得最大值?
(Ⅲ)当V(x)取得最大值时,求异面直线AC与PF所成角的余弦值
推荐套卷
如图所示,等腰△ABC的底边AB=6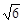 ,高CD=3,点E是线段BD上异于点B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.记
,高CD=3,点E是线段BD上异于点B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.记 ,用
,用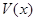 表示四棱锥P-ACFE的体积.
表示四棱锥P-ACFE的体积.
(Ⅰ)求 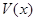 的表达式;
的表达式;
(Ⅱ)当x为何值时,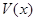 取得最大值?
取得最大值?
(Ⅲ)当V(x)取得最大值时,求异面直线AC与PF所成角的余弦值