根据空气质量指数API(为整数)的不同,可将空气质量分级如下表:

对某城市一年( 365天)的空气质量进行监测,获得的API数据按照区间 进行分组,得到频率分布直方图如下图.
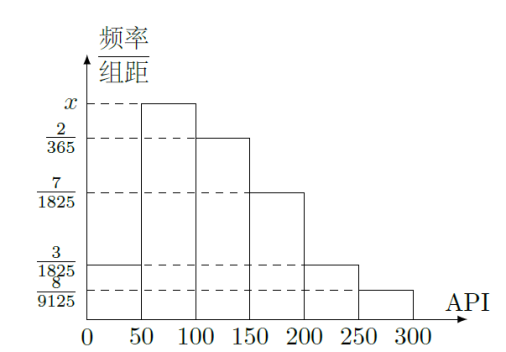
(1)求直方图中 的值;
(2)计算一年中空气质量分别为良和轻微污染的天数;
(3)求该城市某一周至少有 2天的空气质量为良或轻微污染的概率.
(结果用分数表示.已知 )
推荐套卷
根据空气质量指数API(为整数)的不同,可将空气质量分级如下表:

对某城市一年( 365天)的空气质量进行监测,获得的API数据按照区间 进行分组,得到频率分布直方图如下图.

(1)求直方图中 的值;
(2)计算一年中空气质量分别为良和轻微污染的天数;
(3)求该城市某一周至少有 2天的空气质量为良或轻微污染的概率.
(结果用分数表示.已知 )