在平面直角坐标系中, 为原点, 是等腰直角三角形, , ,顶点 ,点 在第一象限,矩形 的顶点 , ,点 在 轴的正半轴上,点 在第二象限,射线 经过点 .
(Ⅰ)如图①,求点 的坐标;
(Ⅱ)将矩形 沿 轴向右平移,得到矩形 ,点 , , , 的对应点分别为 , , , .设 ,矩形 与 重叠部分的面积为 .
①如图②,当点 在 轴正半轴上,且矩形 与 重叠部分为四边形时, 与 相交于点 ,试用含有 的式子表示 ,并直接写出 的取值范围;
②当 时,求 的取值范围(直接写出结果即可).

相关知识点
推荐套卷
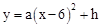 。已知球网与O点的水平距离为9m,高度为2.43m,球场的边界距O点的水平距离为18m。
。已知球网与O点的水平距离为9m,高度为2.43m,球场的边界距O点的水平距离为18m。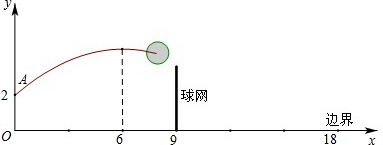
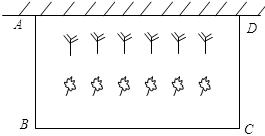
 ,花园的一边靠墙,另三边用总长为40m的栅栏围成(如图所示).若设花园的
,花园的一边靠墙,另三边用总长为40m的栅栏围成(如图所示).若设花园的 (m),花园的面积为
(m),花园的面积为 (m
(m ).
).
 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量
 吗?若能,求出此时
吗?若能,求出此时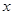 的值;若不能,说明理由;
的值;若不能,说明理由; 的图象交反比例函数
的图象交反比例函数 的图象于点A.B,交
的图象于点A.B,交 轴于点C。
轴于点C。
 的取值范围;
的取值范围;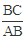 =
=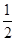 ,求
,求 的图象交于A.B两点.已知当x>1时,y1>y2;当0<x<1时,y1<y2.
的图象交于A.B两点.已知当x>1时,y1>y2;当0<x<1时,y1<y2.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号