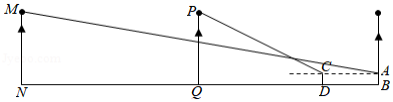
在一次测量物体高度的数学实践活动中,小明从一条笔直公路上选择三盏高度相同的路灯进行测量.如图,他先在点 处安置测倾器,于点 处测得路灯 顶端的仰角为 ,再沿 方向前进10米,到达点 处,于点 处测得路灯 顶端的仰角为 .若测倾器的高度为1.2米,每相邻两根灯柱之间的距离相等,求路灯的高度(结果精确到0.1米).
(参考数据: , , , , ,
相关知识点
推荐套卷
在一次测量物体高度的数学实践活动中,小明从一条笔直公路上选择三盏高度相同的路灯进行测量.如图,他先在点 处安置测倾器,于点 处测得路灯 顶端的仰角为 ,再沿 方向前进10米,到达点 处,于点 处测得路灯 顶端的仰角为 .若测倾器的高度为1.2米,每相邻两根灯柱之间的距离相等,求路灯的高度(结果精确到0.1米).
(参考数据: , , , , ,
