问题提出
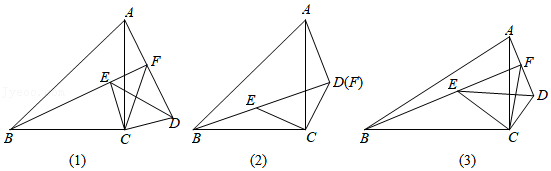
如图（1），在 和 中， ， ， ，点 在 内部，直线 与 于点 ．线段 ， ， 之间存在怎样的数量关系？
问题探究
（1）先将问题特殊化如图（2），当点 ， 重合时，直接写出一个等式，表示 ， ， 之间的数量关系；
（2）再探究一般情形如图（1），当点 ， 不重合时，证明（1）中的结论仍然成立．
问题拓展
如图（3），在 和 中， ， ， 是常数），点 在 内部，直线 与 交于点 ．直接写出一个等式，表示线段 ， ， 之间的数量关系．
如图，经过原点的抛物线y=-x2+bx（b＞2）与x轴的另一交点为A，过点P（1，
）作直线PN⊥x轴于点N，交抛物线于点B．点B关于抛物线对称轴的对称点为C．连结CB，CP．
（1）当b=4时，求点A的坐标及BC的长；
（2）连结CA，求b的适当的值，使得CA⊥CP；
（3）当b=6时，如图2，将△CBP绕着点C按逆时针方向旋转，得到△CB′P′，CP与抛物线对称轴的交点为E，点M为线段B′P′（包含端点）上任意一点，请直接写出线段EM长度的取值范围．
如图1，在△ABC中，∠ACB=90°，BC=2，∠A=30°，点E，F分别是线段BC，AC的中点，连结EF．
（1）线段BE与AF的位置关系是 ，
= ．
（2）如图2，当△CEF绕点C顺时针旋转a时（0°＜a＜180°），连结AF，BE，（1）中的结论是否仍然成立．如果成立，请证明；如果不成立，请说明理由．
（3）如图3，当△CEF绕点C顺时针旋转a时（0°＜a＜180°），延长FC交AB于点D，如果AD=6-2
，求旋转角a的度数．
如图，二次函数y=x2+bx+c经过点（-1，0）和点（0，-3）．
（1）求二次函数的表达式；
（2）如果一次函数y=4x+m的图象与二次函数的图象有且只有一个公共点，求m的值和该公共点的坐标；
（3）将二次函数图象y轴左侧部分沿y轴翻折，翻折后得到的图象与原图象剩余部分组成一个新的图象，该图象记为G，如果直线y=4x+n与图象G有3个公共点，求n的值．
阅读下列材料：
已知：如图1，在Rt△ABC中，∠C=90°，AC=4，BC=3，P为AC边上的一动点，以PB，PA为边构造□APBQ，求对角线PQ的最小值及此时
的值是多少．
在解决这个问题时，小明联想到在学习平行线间的距离时所了解的知识：端点分别在两条平行线上的所有线段中，垂直于平行线的线段最短．进而，小明构造出了如图2的辅助线，并求得PQ的最小值为3．参考小明的做法，解决以下问题：
（1）继续完成阅读材料中的问题：当PQ的长度最小时，= ；
（2）如图3，延长PA到点E，使AE=nPA（n为大于0的常数）．以PE，PB为边作□PBQE，那么对角线PQ的最小值为 ，此时= ；
（3）如图4，如果P为AB边上的一动点，延长PA到点E，使AE=nPA（n为大于0的常数），以PE，PC为边作□PCQE，那么对角线PQ的最小值为 ，此时= ．
，求BE的长．
粤公网安备 44130202000953号