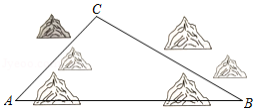
如图，著名旅游景区 位于大山深处，原来到此旅游需要绕行 地，沿折线 方可到达．当地政府为了增强景区的吸引力，发展壮大旅游经济，修建了一条从 地到景区 的笔直公路．请结合 ， ， 千米， ， 等数据信息，解答下列问题：
（1）公路修建后，从 地到景区 旅游可以少走多少千米？
（2）为迎接旅游旺季的到来，修建公路时，施工队使用了新的施工技术，实际工作时每天的工效比原计划增加 ，结果提前50天完成了施工任务．求施工队原计划每天修建多少千米？
|+（2014﹣
）0﹣3tan30°；
，其中
是2x2-2x-7=0的根．如图，在矩形ABCD中，AB＝12cm，BC＝8cm．点E、F、G分别从点A、B、C同时出发，沿矩形的边按逆时针方向移动，点E、G的速度均为2cm/s，点F的速度为4cm/s，当点F追上点G（即点F与点G重合）时，三个点随之停止移动．设移动开始后第ts时，△EFG的面积为Scm2．
（1）当
＝1s时，S的值是多少？
（2） 当
时，点E、F、G分别在边AB、BC、CD上移动，用含t的代数式表示S；当
时，点E在边AB上移动，点F、G都在边CD上移动，用含t的代数式表示S．
（3）若点F在矩形的边BC上移动，当为何值时，以点B、E、F为顶点的三角形与以C、F、G为顶点的三角形相似？请说明理由
如图，在平面直角坐标系中，已知点A的坐标是（4，0），并且OA=OC=4OB，动点P在过A，B，C三点的抛物线上．
（1）求抛物线的解析式；
（2）在抛物线上是否存在点P，使得∠PCO=∠POC？若存在，求出符合条件的点P的坐标；若不存在，说明理由；
（3）是否存在点P，使得△ACP是以AC为直角边的直角三角形？若存在，求出所有符合条件的点P的坐标；若不存在，说明理由；
如图，△ABC中，AB＝AC，以AC为直径的⊙O与边BC交于点E．过E作直线与AB垂直，垂足为F，且与AC的延长线交于点G．
（1）判断直线FG与⊙O的位置关系，并证明你的结论；
（2）若BF＝1，CG＝2，求⊙O半径．
粤公网安备 44130202000953号