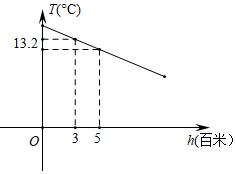
某地区山峰的高度每增加1百米,气温大约降低 ,气温 和高度 (百米)的函数关系如图所示.
请根据图象解决下列问题:
(1)求高度为5百米时的气温;
(2)求 关于 的函数表达式;
(3)测得山顶的气温为 ,求该山峰的高度.
相关知识点
推荐套卷
某地区山峰的高度每增加1百米,气温大约降低 ,气温 和高度 (百米)的函数关系如图所示.
请根据图象解决下列问题:
(1)求高度为5百米时的气温;
(2)求 关于 的函数表达式;
(3)测得山顶的气温为 ,求该山峰的高度.
