为了帮助九年级学生做好体育考试项目的选考工作，某校统计了本县上届九年级毕业生体育考试各个项目参加的男、女生人数及平均成绩，并绘制成如图两个统计图，请结合统计图信息解决问题．
（1）“掷实心球”项目男、女生总人数是“跳绳”项目男、女生总人数的2倍，求“跳绳”项目的女生人数；
（2）若一个考试项目的男、女生总平均成绩不小于9分为“优秀”，试判断该县上届毕业生的考试项目中达到“优秀”的有哪些项目，并说明理由；
（3）请结合统计图信息和实际情况，给该校九年级学生体育考试项目的选择提出合理化建议．
相关试题
。
如图，某中学初三（2）班数学活动小组利用周日开展课外实践活动，他们要在湖面上测量建在地面上某塔AB的高度．如图，在湖面上点C测得塔顶A的仰角为45°，沿直线CD向塔AB方向前进18米到达点D，测得塔顶A的仰角为60度．已知湖面低于地平面1米，请你帮他们计算出塔AB的高度．（结果保留根号）
如图1，在⊙O中，E是弧AB的中点，C为⊙O上的一动点（C与E在AB异侧），连接EC交AB于点F，EB=
（r是⊙O的半径）．
（1）D为AB延长线上一点，若DC=DF，证明：OC⊥CD；
（2）如图2，当F是AB的四等分点且EF·EC=
时，求EC的值．
=
，连接AB、AD、BD，弦AB不经过圆心O，延长AB到E，使BE=AB，连接EC，F是EC的中点，连接BF．
BD；相关知识点
推荐套卷
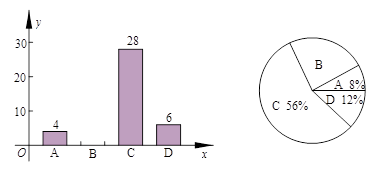
粤公网安备 44130202000953号