如果将四根木条首尾相连,在相连处用螺钉连接,就能构成一个平面图形.
(1)若固定三根木条 , , 不动, , ,如图,量得第四根木条 ,判断此时 与 是否相等,并说明理由.
(2)若固定二根木条 、 不动, , ,量得木条 , ,写出木条 的长度可能取得的一个值(直接写出一个即可)
(3)若固定一根木条 不动, ,量得木条 ,如果木条 , 的长度不变,当点 移到 的延长线上时,点 也在 的延长线上;当点 移到 的延长线上时,点 、 、 能构成周长为 的三角形,求出木条 , 的长度.

相关知识点
推荐套卷
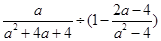 ),其中
),其中 .
.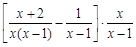 ,其中
,其中 .
.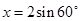 ,先化简
,先化简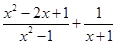 ,再求它的值;
,再求它的值;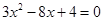 的两根,求
的两根,求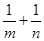 .
.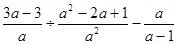 ,其中
,其中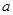 =2.
=2.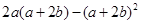 ,其中
,其中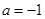 ,
,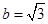 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号