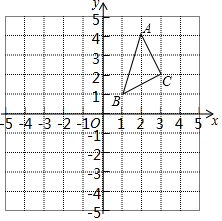
在边长为 1 个单位长度的正方形网格中建立如图所示的平面直角坐标系, 的顶点都在格点上, 请解答下列问题:
(1) 作出 向左平移 4 个单位长度后得到的△ ,并写出点 的坐标;
(2) 作出 关于原点 对称的△ ,并写出点 的坐标;
(3) 已知 关于直线 对称的△ 的顶点 的坐标为 ,请直接写出直线 的函数解析式 .
推荐套卷
在边长为 1 个单位长度的正方形网格中建立如图所示的平面直角坐标系, 的顶点都在格点上, 请解答下列问题:
(1) 作出 向左平移 4 个单位长度后得到的△ ,并写出点 的坐标;
(2) 作出 关于原点 对称的△ ,并写出点 的坐标;
(3) 已知 关于直线 对称的△ 的顶点 的坐标为 ,请直接写出直线 的函数解析式 .
