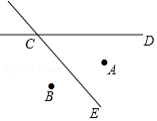
两个城镇 ， 与一条公路 ，一条河流 的位置如图所示，某人要修建一避暑山庄，要求该山庄到 ， 的距离必须相等，到 和 的距离也必须相等，且在 的内部，请画出该山庄的位置 ．（不要求写作法，保留作图痕迹．
=3的解为x=1，求a的值．
-
=3，求
的值．
……
.相关知识点
推荐套卷
两个城镇 ， 与一条公路 ，一条河流 的位置如图所示，某人要修建一避暑山庄，要求该山庄到 ， 的距离必须相等，到 和 的距离也必须相等，且在 的内部，请画出该山庄的位置 ．（不要求写作法，保留作图痕迹．
粤公网安备 44130202000953号