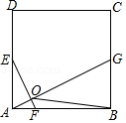
如图,在正方形 中,点 、 分别是边 、 的中点, .
(1)求证: ;
(2)若点 、 分别在射线 、 上同时向右、向上运动,点 运动速度是点 运动速度的2倍, 是否成立(只写结果,不需说明理由)?
(3)正方形 的边长为4, 是正方形 内一点,当 ,求 周长的最小值.
相关知识点
推荐套卷
如图,在正方形 中,点 、 分别是边 、 的中点, .
(1)求证: ;
(2)若点 、 分别在射线 、 上同时向右、向上运动,点 运动速度是点 运动速度的2倍, 是否成立(只写结果,不需说明理由)?
(3)正方形 的边长为4, 是正方形 内一点,当 ,求 周长的最小值.
