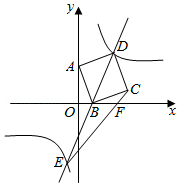
如图,在平面直角坐标系中,已知点 的坐标为 ,点 的坐标为 ,连结 ,以 为边在第一象限内作正方形 ,直线 交双曲线 于 、 两点,连结 ,交 轴于点 .
(1)求双曲线 和直线 的解析式.(2)求 的面积.
相关知识点
推荐套卷
如图,在平面直角坐标系中,已知点 的坐标为 ,点 的坐标为 ,连结 ,以 为边在第一象限内作正方形 ,直线 交双曲线 于 、 两点,连结 ,交 轴于点 .
(1)求双曲线 和直线 的解析式.(2)求 的面积.
