1471年，德国数学家米勒提出了雕塑问题：假定有一个雕塑高AB=3米，立在一个底座上，底座的高BC=2.2米，一个人注视着这个雕塑并朝它走去，这个人的水平视线离地1.7米，问此人应站在离雕塑底座多远处，才能使看雕塑的效果最好，所谓看雕塑的效果最好是指看雕塑的视角最大，问题转化为在水平视线EF上求使视角最大的点，如图：过A、B两点，作一圆与EF相切于点M，你能说明点M为所求的点吗？并求出此时这个人离雕塑底座的距离？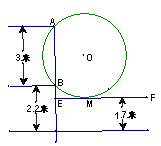
相关试题
某服装厂承揽一项生产夏凉小衫1600件的任务，计划用t天完成。
（1）写出每天生产夏凉小衫w（件）与生产时间t（天）（t＞4）之间的函数关系式；
（2）由于气温提前升高，商家与服装厂商议调整计划，决定提前4天交货，那么服装厂每天要做多少件夏凉小衫才能完成任务？
.
如图，正方形ABCD的边长为4，E是BC边的中点，点P在射线AD上，过P作PF⊥AE于F．
（1）求证：△PFA∽△ABE；
（2）若AP=
，求△PFA的面积
，标杆与旗杆的水平距离
，人的眼睛与地面的高度
，人与标杆CD的水平距离
，求旗杆
的高度．
相关知识点
推荐套卷
粤公网安备 44130202000953号