如图,抛物线过点 和 ,顶点为 ,直线 与抛物线的对称轴 的交点为 , ,平行于 轴的直线 与抛物线交于点 ,与直线 交于点 ,点 的横坐标为 ,四边形 为平行四边形.
(1)求点 的坐标及抛物线的解析式;
(2)若点 为抛物线上的动点,且在直线 上方,当 面积最大时,求点 的坐标及 面积的最大值;
(3)在抛物线的对称轴上取一点 ,同时在抛物线上取一点 ,使以 为一边且以 , , , 为顶点的四边形为平行四边形,求点 和点 的坐标.

相关知识点
推荐套卷
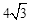 ,直角边CD在y轴上,且点C与点A重合.Rt△CDE沿y轴正方向平行移动,当点C运动到点O时停止运动.解答下列问题:
,直角边CD在y轴上,且点C与点A重合.Rt△CDE沿y轴正方向平行移动,当点C运动到点O时停止运动.解答下列问题: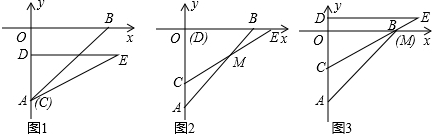

 OABC一起先向右平移4个单位后,再向下平移m(0<m<3)个单位,得到抛物线W′和
OABC一起先向右平移4个单位后,再向下平移m(0<m<3)个单位,得到抛物线W′和 (a>0)与x轴交于A、B两点(A在B的左侧),与y轴交于点C,点D的坐标为(﹣6,0),且∠ACD=90°.
(a>0)与x轴交于A、B两点(A在B的左侧),与y轴交于点C,点D的坐标为(﹣6,0),且∠ACD=90°.

 粤公网安备 44130202000953号
粤公网安备 44130202000953号