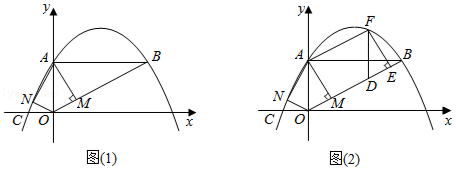如图（1），在平面直角坐标系中，抛物线 与y轴交于点A，与x轴交于点 ，且经过点B（8，4），连接AB，BO，作 于点M，将 沿y轴翻折，点M的对应点为点N．解答下列问题：
（1）抛物线的解析式为 ，顶点坐标为 ；
（2）判断点N是否在直线AC上，并说明理由；
（3）如图（2），将图（1）中 沿着OB平移后，得到 ．若DE边在线段OB上，点F在抛物线上，连接AF，求四边形 的面积．
相关试题
，求代数式
的值．
在平面直角坐标系xOy中，直线
分别与x轴，y轴交于过点A，B，点C是第一象限内的一点，且AB=AC，AB⊥AC，抛物线
经过A，C两点，与
轴的另一交点为D．
（1）求此抛物线的解析式；
（2）判断直线AB与CD的位置关系，并证明你的结论；
（3）点M为x轴上一动点，在抛物线上是否存在一点N，使以A,B,M,N四点构成的四边形为平行四边形？若存在，求点N的坐标；若不存在，请说明理由．
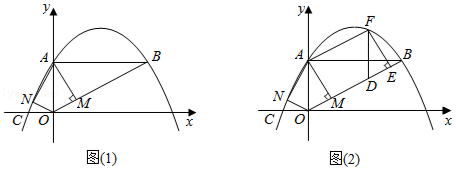
相关知识点
推荐套卷
粤公网安备 44130202000953号