为庆祝中华人民共和国七十周年华诞，某校举行书画大赛，准备购买甲、乙两种文具，奖励在活动中表现优秀的师生．已知购买2个甲种文具、1个乙种文具共需花费35元；购买1个甲种文具、3个乙种文具共需花费30元．
（1）求购买一个甲种文具、一个乙种文具各需多少元？
（2）若学校计划购买这两种文具共120个，投入资金不少于955元又不多于1000元，设购买甲种文具 个，求有多少种购买方案？
（3）设学校投入资金 元，在（2）的条件下，哪种购买方案需要的资金最少？最少资金是多少元？
相关试题
如图，有四条互相不平行的直线L1、L2、L3、L4所截出的八个角．请你任意选择其中的三个角（不可选择未标注的角），尝试找到它们的关系，并选择其中一组予以证明．
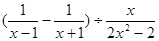，然后从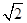
，1，－1中选取一个你认为合适的数作为x的值代入求值．抛物线y=－x2＋bx＋c经过点A、B、C，已知A（－1，0），C（0，3）．
（1）求抛物线的解析式；
（2）求点B的坐标及直线BC的解析式；
（3）如图，P为线段BC上一点，过点P作y轴平行线，交抛物线于点D，求△BDC的面积的最大值。
相关知识点
推荐套卷
粤公网安备 44130202000953号