为了参加学校举行的传统文化知识竞赛，某班进行了四次模拟训练，将成绩优秀的人数和优秀率绘制成如下两个不完整的统计图：
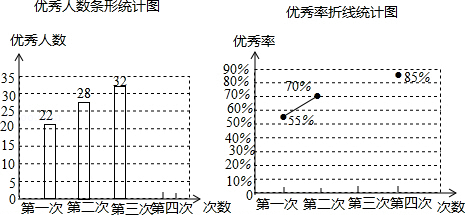
请根据以上两图解答下列问题：
（1）该班总人数是 ；
（2）根据计算，请你补全两个统计图；
（3）观察补全后的统计图，写出一条你发现的结论．
相关试题
，AB的中垂线
交
于点
，交
于点
， 
平分
.
∽
； 
的值；
的值；
，
，求
；
，
，求
（用m、n表示）.
的边
在
的边
上，顶点
、
分别在边
、
上，
，垂足为
．已知
，
.
为正方形时，求该正方形的边长；
面积为18时，求矩形的长和宽．
中，
，
，
，求（1）
的值. 
中，
、
、
分别是
、AC、BC上的点，联结
、EF交于点G，且
.
相似的三角形（不用证明）；
，试求
的值．
推荐套卷
为了参加学校举行的传统文化知识竞赛，某班进行了四次模拟训练，将成绩优秀的人数和优秀率绘制成如下两个不完整的统计图：
请根据以上两图解答下列问题：
（1）该班总人数是 ；
（2）根据计算，请你补全两个统计图；
（3）观察补全后的统计图，写出一条你发现的结论．
粤公网安备 44130202000953号