如图,直线 、 为常数)分别与 轴、 轴交于点 、 ,抛物线 与 轴交于点 .
(1)求直线 的函数解析式;
(2)若点 是抛物线 上的任意一点,设点 到直线 的距离为 ,求 关于 的函数解析式,并求 取最小值时点 的坐标;
(3)若点 在抛物线 的对称轴上移动,点 在直线 上移动,求 的最小值.
推荐套卷
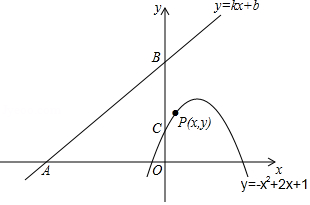
如图,直线 、 为常数)分别与 轴、 轴交于点 、 ,抛物线 与 轴交于点 .
(1)求直线 的函数解析式;
(2)若点 是抛物线 上的任意一点,设点 到直线 的距离为 ,求 关于 的函数解析式,并求 取最小值时点 的坐标;
(3)若点 在抛物线 的对称轴上移动,点 在直线 上移动,求 的最小值.
