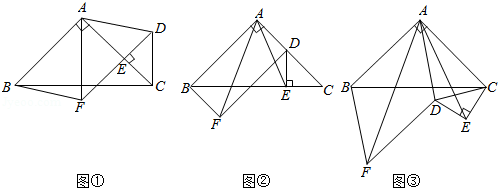
如图①，在 中， ， ，点 在 上（且不与点 ， 重合），在 的外部作 ，使 ， ，连接 ，分别以 ， 为邻边作平行四边形 ，连接 ．
（1）请直接写出线段 ， 的数量关系 ；
（2）将 绕点 逆时针旋转，当点 在线段 上时，如图②，连接 ，请判断线段 ， 的数量关系，并证明你的结论；
（3）在图②的基础上，将 绕点 继续逆时针旋转，请判断（2）问中的结论是否发生变化？若不变，结合图③写出证明过程；若变化，请说明理由．
相关试题
的顶点为坐标原点
，焦点
，(1)求抛物线
作直线交抛物线
、
两点，若直线
与
分别交直线
于
、
两点，当
时，求直线
的方程。
，
．
在区间
上单调递增，求
的取值范围；
的前
项和为
，且
，其中
，数列
的前
，求证：
，
，
，
，
为
的中点，把三角形
沿
折起至
位置，使得
，
是线段
的中点.
；
面
；
的体积.
（月）
（千克）
关于变量
的线性回归直线方程
．
，
）推荐套卷
如图①，在 中， ， ，点 在 上（且不与点 ， 重合），在 的外部作 ，使 ， ，连接 ，分别以 ， 为邻边作平行四边形 ，连接 ．
（1）请直接写出线段 ， 的数量关系 ；
（2）将 绕点 逆时针旋转，当点 在线段 上时，如图②，连接 ，请判断线段 ， 的数量关系，并证明你的结论；
（3）在图②的基础上，将 绕点 继续逆时针旋转，请判断（2）问中的结论是否发生变化？若不变，结合图③写出证明过程；若变化，请说明理由．
粤公网安备 44130202000953号