如图，在平面直角坐标系中，有一Rt△ABC，且A（－1，3），B（－3，－1），
C（－3，3），已知△A1AC1是由△ABC旋转得到的．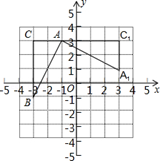
（1）请写出旋转中心的坐标是 ，旋转角是 度；
（2）以（1）中的旋转中心为中心，画出△A1AC1顺时针旋转90°的三角形．
的二元一次方程组
的解是正整数，求整数
的值。
的正整数解是方程
的解，求
的值。
为实数，且
，求
的平方根。
□ABCD中，
于点E，
于点F
相关知识点
推荐套卷
如图，在平面直角坐标系中，有一Rt△ABC，且A（－1，3），B（－3，－1），
C（－3，3），已知△A1AC1是由△ABC旋转得到的．
（1）请写出旋转中心的坐标是 ，旋转角是 度；
（2）以（1）中的旋转中心为中心，画出△A1AC1顺时针旋转90°的三角形．
粤公网安备 44130202000953号