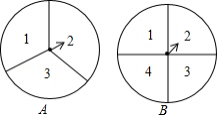
如图，转盘 的三个扇形面积相等，分别标有数字1，2，3，转盘 的四个扇形面积相等，分别有数字1，2，3，4．转动 、 转盘各一次，当转盘停止转动时，将指针所落扇形中的两个数字相乘（当指针落在四个扇形的交线上时，重新转动转盘）．
（1）用树状图或列表法列出所有可能出现的结果；
（2）求两个数字的积为奇数的概率．
已知抛物线y=x²-4x+3．
（1）该抛物线的对称轴是 ，顶点坐标 ；
（2）将该抛物线向上平移2个单位长度，再向左平移3个单位长度得到新的二次函数图像，请写出相应的解析式，并用列表，描点，连线的方法画出新二次函数的图像；
| x |
… |
|
|
|
|
|
… |
| y |
… |
|
|
|
|
|
… |
（3）新图像上两点A（x1，y1），B（x2，y2），它们的横坐标满足＜-2，且-1＜＜0，试比较y1，y2，0三者的大小关系．
如图，已知⊙O的半径为4，CD为⊙O的直径，AC为⊙O的弦，B为CD延长线上的一点，∠ABC=30°，且AB=AC。
（1）求证：AB是⊙O的切线；
（2）求弦AC的长；
（3）求图中阴影部分的面积。
雅安地震牵动全国人民的心，某单位开展了“一方有难，八方支援”赈灾捐款活动，第一天收到捐款10000元，第三天收到捐款12100元。
（1）如果第二天，第三天收到捐款的增长率相同，求捐款的平均增长率；
（2）按照（1）中收到捐款的增长率速度，第四天该单位能收到多少元的捐款？
某中学举行“中国梦，我的梦”演讲比赛，九年级（1）班的班长和学习委员都想去，于是他们用摸球游戏决定谁去参加，游戏规则是：在一个不透明的袋子里有除数字外完全相同的4个小球，上面分别标有数字1,2,3,4，一人先从袋中随机摸出一个小球，另一个人再从袋中剩下的3个小球中随机摸出一个小球。
（1）请列出所有可能出现的结果；（可考虑用树形图、列表等方法）
（2）若摸出的两个小球上的数字和为偶数，则班长去参赛，请问他能如愿的概率是多少？
粤公网安备 44130202000953号