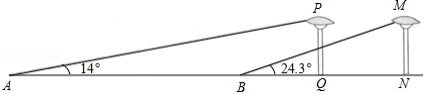
如图,在某街道路边有相距 、高度相同的两盏路灯(灯杆垂直地面),小明为了测量路灯的高度,在地面 处测得路灯 的顶端仰角为 ,向前行走 到达 处,在地面测得路灯 的顶端仰角为 ,已知点 , , , 在同一条直线上,请你利用所学知识帮助小明求出路灯的高度.(结果精确到 .参考数据: , , , , ,
相关知识点
推荐套卷
如图,在某街道路边有相距 、高度相同的两盏路灯(灯杆垂直地面),小明为了测量路灯的高度,在地面 处测得路灯 的顶端仰角为 ,向前行走 到达 处,在地面测得路灯 的顶端仰角为 ,已知点 , , , 在同一条直线上,请你利用所学知识帮助小明求出路灯的高度.(结果精确到 .参考数据: , , , , ,
