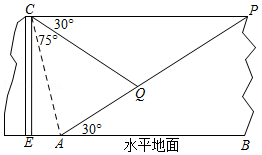
如图，某地质公园中有两座相邻小山．游客需从左侧小山山脚 处乘坐竖直观光电梯上行100米到达山顶 处，然后既可以沿水平观光桥步行到景点 处，也可以通过滑行索道到达景点 处，在山顶 处观测坡底 的俯角为 ，观测 处的俯角为 ，已知右侧小山的坡角为 （图中的点 ， ， ， ， ， 均在同一平面内，点 ， ， 在同一直线上）
（1）求 的度数及 的长度；
（2）求 ， 两点之间的距离．（结果保留根号）
相关试题
如图，长方体的底面是边长为2cm的正方形，高是6cm．
（1）如果用一根细线从点A开始经过4个侧面围绕一圈到达点B．那么所用的细线最短长度是多少厘米？
（2）如果从A点开始经过4个侧面缠绕2圈到达点B，那么所用细线最短长度是多少厘米？
甲、乙两船从位于南北走向的海岸线上的港口A同时出发，甲以每小时15海里的速度向北偏东40°方向航行，乙船以每小时20海里的速度向另一方向航行，4小时后甲船到达C岛，乙船到达B岛，已知B、C两岛相距100海里，判断乙船航行的方向，并说明理由．
πr3，r为球的半径，结果精确到0．01cm）．相关知识点
推荐套卷
粤公网安备 44130202000953号