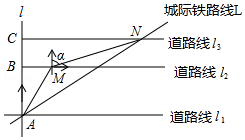
如图为某区域部分交通线路图,其中直线 ,直线 与直线 、 、 都垂直,垂足分别为点 、点 和点 ,(高速路右侧边缘), 上的点 位于点 的北偏东 方向上,且 千米, 上的点 位于点 的北偏东 方向上,且 , 千米,点 和点 是城际线 上的两个相邻的站点.
(1)求 和 之间的距离;
(2)若城际火车平均时速为150千米 小时,求市民小强乘坐城际火车从站点 到站点 需要多少小时?(结果用分数表示)
相关知识点
推荐套卷
如图为某区域部分交通线路图,其中直线 ,直线 与直线 、 、 都垂直,垂足分别为点 、点 和点 ,(高速路右侧边缘), 上的点 位于点 的北偏东 方向上,且 千米, 上的点 位于点 的北偏东 方向上,且 , 千米,点 和点 是城际线 上的两个相邻的站点.
(1)求 和 之间的距离;
(2)若城际火车平均时速为150千米 小时,求市民小强乘坐城际火车从站点 到站点 需要多少小时?(结果用分数表示)
