为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.李明按照相关政策投资销售本市生产的一种新型节能灯.已知这种节能灯的成本价为每件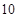 元,出厂价为每件
元,出厂价为每件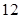 元,每月销售量
元,每月销售量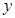 (件)与销售单价
(件)与销售单价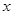 (元)之间的关系近似满足一次函数:
(元)之间的关系近似满足一次函数: 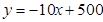 .
.
(1)李明在开始创业的第一个月将销售单价定为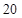 元,那么政府这个月为他承担的总差价为多少元?
元,那么政府这个月为他承担的总差价为多少元?
(2)设李明获得的利润为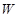 (元),当销售单价定为多少元时,每月可获得最大利润?
(元),当销售单价定为多少元时,每月可获得最大利润?
(3)物价部门规定,这种节能灯的销售单价不得高于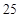 元.如果李明想要每月获得的利润不低于
元.如果李明想要每月获得的利润不低于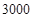 元,那么政府为他承担的总差价最少为多少元?
元,那么政府为他承担的总差价最少为多少元?