如图,在10×10的正方形网格中（每个小正方形的边长都为1个单位）,△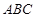
的三个顶点都在格点上.
（1）建立如图所示的直角坐标系,请在图中标出△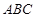的外接圆的圆心
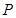的位置,并填写:
①圆心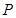的坐标:（_______,_______）;
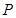②⊙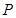的半径为_______ ．
（2）将△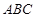绕点
逆时针旋转
得到△
,画出图形,并求线段
扫过的图形的面积．
=x-
(4-y)=
(y+3)
=
-1=
推荐套卷
如图,在10×10的正方形网格中（每个小正方形的边长都为1个单位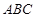）,△的三个顶点都在格点上.
（1）建立如图所示的直角坐标系,请在图中标出△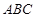的外接圆的圆心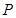的位置,并填写:
①圆心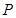的坐标:（_______,_______）;
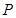②⊙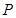的半径为_______ ．
（2）将△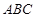绕点逆时针旋转得到△,画出图形,并求线段扫过的图形的面积．
粤公网安备 44130202000953号