抛物线 与 轴交于点 ， 在 的左侧），与 轴交于点 ．
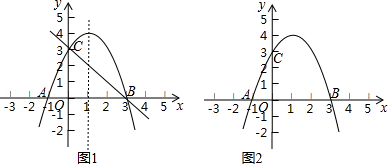
（1）求直线 的解析式；
（2）抛物线的对称轴上存在点 ，使 ，利用图1求点 的坐标；
（3）点 在 轴右侧的抛物线上，利用图2比较 与 的大小，并说明理由．
相关试题
的绳子，围成矩形场地，矩形的一边长为
m，面积为
m
.
是正三角形
内的一点，且
， 
，
．若将
绕点
逆时针旋转后，得到
．
之间的距离；
的度数．
中，过点
作
，垂足为
，连接
，
为线段
．
∽
；
，求
的长．
的图象过点A（3，0），B（-1，0）且与y轴交点为C（0，6）.相关知识点
推荐套卷
抛物线 与 轴交于点 ， 在 的左侧），与 轴交于点 ．
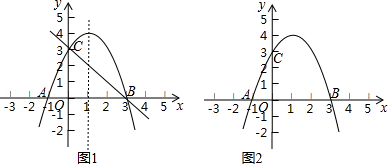
（1）求直线 的解析式；
（2）抛物线的对称轴上存在点 ，使 ，利用图1求点 的坐标；
（3）点 在 轴右侧的抛物线上，利用图2比较 与 的大小，并说明理由．
粤公网安备 44130202000953号