如图，抛物线y=ax2+bx（a＞0）与双曲线y=
相交于点A，B．已知点B的坐标为（﹣2，﹣2），点A在第一象限内，且tan∠AOx=4．过点A作直线AC∥x轴，交抛物线于另一点C．
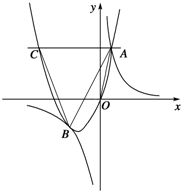
（1）求双曲线和抛物线的解析式；
（2）计算△ABC的面积；
（3）在抛物线上是否存在点D，使△ABD的面积等于△ABC的面积．若存在，请你写出点D的坐标；若不存在，请你说明理由．
相关试题
+（﹣2014）0；如图，在平面直角坐标系中，抛物线y=ax2+bx+4与x轴的一个交点为A（-2，0），与y轴的交点为C，对称轴是x=3，对称轴与x轴交于点B．
（1）求抛物线的函数表达式；
（2）经过B，C的直线l平移后与抛物线交于点M，与x轴交于点N，当以B，C，M，N为顶点的四边形是平行四边形时，求出点M的坐标；
（3）若点D在x轴上，在抛物线上是否存在点P，使得△PBD≌△PBC？若存在，直接写出点P的坐标；若不存在，请说明理由．
如图1，在Rt△ABC中，∠ACB=90°，AB=10，BC=6，扇形纸片DOE的顶点O与边AB的中点重合，OD交BC于点F，OE经过点C，且∠DOE=∠B．
（1）证明△COF是等腰三角形，并求出CF的长；
（2）将扇形纸片DOE绕点O逆时针旋转，OD，OE与边AC分别交于点M，N（如图2），当CM的长是多少时，△OMN与△BCO相似？
已知AB是半圆O的直径，点C是半圆O上的动点，点D是线段AB延长线上的动点，在运动过程中，保持CD=OA．
（1）当直线CD与半圆O相切时（如图①），求∠ODC的度数；
（2）当直线CD与半圆O相交时（如图②），设另一交点为E，连接AE，若AE∥OC，
①AE与OD的大小有什么关系？为什么？
②求∠ODC的度数．
相关知识点
推荐套卷
粤公网安备 44130202000953号