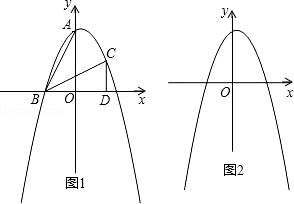
在直角坐标系 中, 、 ,将 经过旋转、平移变化后得到如图1所示的 .
(1)求经过 、 、 三点的抛物线的解析式;
(2)连接 ,点 是位于线段 上方的抛物线上一动点,若直线 将 的面积分成 两部分,求此时点 的坐标;
(3)现将 、 分别向下、向左以 的速度同时平移,求出在此运动过程中 与 重叠部分面积的最大值.
相关知识点
推荐套卷
在直角坐标系 中, 、 ,将 经过旋转、平移变化后得到如图1所示的 .
(1)求经过 、 、 三点的抛物线的解析式;
(2)连接 ,点 是位于线段 上方的抛物线上一动点,若直线 将 的面积分成 两部分,求此时点 的坐标;
(3)现将 、 分别向下、向左以 的速度同时平移,求出在此运动过程中 与 重叠部分面积的最大值.
