如图1,将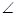 EAF绕着四边形ABCD的顶点A顺时针旋转,
EAF绕着四边形ABCD的顶点A顺时针旋转,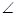 EAF的两边分别与DC的延长线交于点F,与CB的延长线交于点E,连接EF。
EAF的两边分别与DC的延长线交于点F,与CB的延长线交于点E,连接EF。
若四边形ABCD为正方形,当
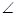 EAF=
EAF=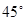 时,EF与DF、BE之间有怎样的数量关系?(只需直接写出结论)
时,EF与DF、BE之间有怎样的数量关系?(只需直接写出结论)如图2,如果四边形ABCD中,AB=AD,
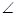 ABC与
ABC与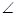 ADC互补,当
ADC互补,当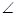 EAF=
EAF= 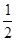
 BAD时,EF与DF、BE之间有怎样的数量关系?请写出它们之间的关系式并给予证明。
BAD时,EF与DF、BE之间有怎样的数量关系?请写出它们之间的关系式并给予证明。在(2)中,若BC=4,DC=7,CF=2,求
 CEF的周长(直接写出结果即可)。
CEF的周长(直接写出结果即可)。
相关知识点
推荐套卷
 cm,AD=4cm.若⊙O与矩形ABCD沿l1同时向右移动,⊙O的移动速度为3cm/s,矩形ABCD的移动速度为4cm/s,设移动时间为t(s).
cm,AD=4cm.若⊙O与矩形ABCD沿l1同时向右移动,⊙O的移动速度为3cm/s,矩形ABCD的移动速度为4cm/s,设移动时间为t(s).

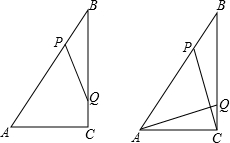

 ,求BG的长.
,求BG的长.
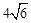 ,求BG的长.
,求BG的长. 粤公网安备 44130202000953号
粤公网安备 44130202000953号