有一块直角三角形纸片,两直角边AC=6cm,BC=8cm。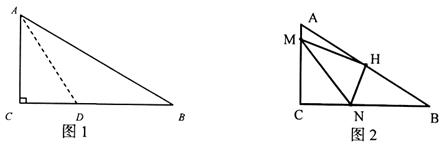
如图1,现将纸片沿直线AD折叠,使直角边AC落在斜边AB上,且与AB重合,则CD= 。
如图2,若将直角
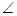 C沿MN折叠,使点C落在AB中点H上,点M、N分别在AC、BC上,则
C沿MN折叠,使点C落在AB中点H上,点M、N分别在AC、BC上,则 、
、 与
与 之间有怎样的数量关系?并证明你的结论。
之间有怎样的数量关系?并证明你的结论。
相关知识点
推荐套卷
有一块直角三角形纸片,两直角边AC=6cm,BC=8cm。
如图1,现将纸片沿直线AD折叠,使直角边AC落在斜边AB上,且与AB重合,则CD= 。
如图2,若将直角
 C沿MN折叠,使点C落在AB中点H上,点M、N分别在AC、BC上,则
C沿MN折叠,使点C落在AB中点H上,点M、N分别在AC、BC上,则 、
、 与
与 之间有怎样的数量关系?并证明你的结论。
之间有怎样的数量关系?并证明你的结论。