若抛物线 (a,b,c是常数, )与直线l都经过y轴上的一点P,且抛物线L的顶点Q在直线l上,则称此直线l与该抛物线L具有“一带一路”关系.此时,直线l叫做抛物线L的“带线”,抛物线L叫做直线l的“路线”.
(1)若直线 与抛物线 具有“一带一路”关系,求m,n的值;
(2)若某“路线”L的顶点在反比例函数 的图象上,它的“带线”l的解析式为 ,求此“路线”L的解析式;
(3)当常数k满足 时,求抛物线 的“带线”l与x轴,y轴所围成的三角形面积的取值范围.
相关知识点
推荐套卷
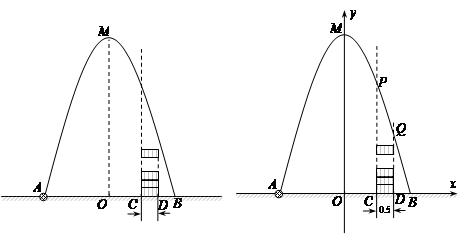
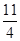 ),与过T点(0,
),与过T点(0,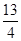 )且平行于x轴的直线距离相等,设点P的坐标为(x,y)
)且平行于x轴的直线距离相等,设点P的坐标为(x,y) 为线段
为线段 (点O为坐标原点)上的一个动点,过
(点O为坐标原点)上的一个动点,过 轴上一点
轴上一点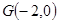 作
作 的垂线,垂足为
的垂线,垂足为 ,直线
,直线 交
交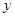 轴于点
轴于点 ,当
,当 ②
② ,其中有且只有一个结论是正确的,请你判断哪个结论正确,并证明.
,其中有且只有一个结论是正确的,请你判断哪个结论正确,并证明.
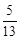 ,cos22°37′=
,cos22°37′= ,tan22°37′=
,tan22°37′=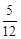 )
) (冲锋舟与汽车速度的比),然后再派冲锋舟前往B(如图2).请你说明理由!
(冲锋舟与汽车速度的比),然后再派冲锋舟前往B(如图2).请你说明理由!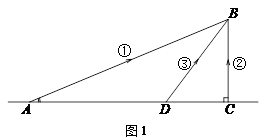


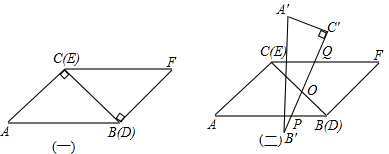
 .
.
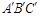 位置,直线
位置,直线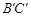 与AB、CF分别相交于P、Q两点,猜想OQ、OP长度的大小关系,并证明你的猜想.
与AB、CF分别相交于P、Q两点,猜想OQ、OP长度的大小关系,并证明你的猜想. 粤公网安备 44130202000953号
粤公网安备 44130202000953号