如图，△ABC与△DEF是两个全等的等腰直角三角形，∠BAC=∠D=90°，AB=AC=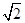
．现将△DEF与△ABC按如图所示的方式叠放在一起．现将△ABC保持不动，△DEF运动，且满足：点E在边BC上运动（不与B、C重合），且边DE始终经过点A，EF与AC交于M点．请问：在△DEF运动过程中，△AEM能否构成等腰三角形？若能，请求出BE的长；若不能，请说明理由．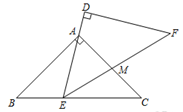
相关试题
，由于甲看错了方程（1）中的a得到方程组的解为
，乙看错了方程（2）中的b得到方程组的解为
若按正确的a．b计算，求原方程组的解
≤1（2）
（2）
相关知识点
推荐套卷
如图，△ABC与△DEF是两个全等的等腰直角三角形，∠BAC=∠D=90°，AB=AC=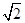．现将△DEF与△ABC按如图所示的方式叠放在一起．现将△ABC保持不动，△DEF运动，且满足：点E在边BC上运动（不与B、C重合），且边DE始终经过点A，EF与AC交于M点．请问：在△DEF运动过程中，△AEM能否构成等腰三角形？若能，请求出BE的长；若不能，请说明理由．
粤公网安备 44130202000953号