已知抛物线 ,顶点为 A,且经过点 ,点 .
(1)求抛物线的解析式;
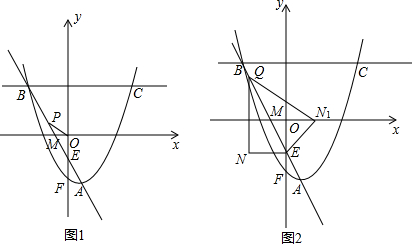
(2)如图1,直线 AB与 x轴相交于点 M, y轴相交于点 E,抛物线与 y轴相交于点 F,在直线 AB上有一点 P,若∠ OPM=∠ MAF,求△ POE的面积;
(3)如图2,点 Q是折线 A﹣ B﹣ C上一点,过点 Q作 QN∥ y轴,过点 E作 EN∥ x轴,直线 QN与直线 EN相交于点 N,连接 QE,将△ QEN沿 QE翻折得到△ QEN 1,若点 N 1落在 x轴上,请直接写出 Q点的坐标.
相关知识点
推荐套卷
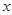 的方程
的方程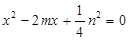 ,其中
,其中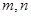 分别是一个等腰三角形的腰和底的长,求证这个方程有两个不相等的实数根.
分别是一个等腰三角形的腰和底的长,求证这个方程有两个不相等的实数根.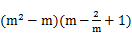 的值.
的值. ∠BAC,过点D作DE⊥AB,DE恰好是∠ADB的平分线,求证:CD=
∠BAC,过点D作DE⊥AB,DE恰好是∠ADB的平分线,求证:CD=
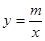 的图象交于A(2,3),B(-3,n)两点.
的图象交于A(2,3),B(-3,n)两点.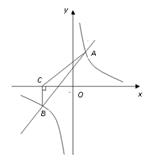
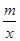 的解集______________;
的解集______________; 粤公网安备 44130202000953号
粤公网安备 44130202000953号