如图,在网格中、建立了平面直角坐标系,每个小正方形的边长均为1个单位长度,将四边形ABCD绕坐标原点O按顺时针方向旋转180°后得到四边形A1B1C1D1.
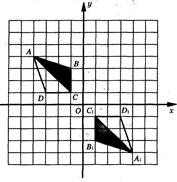
(1)写出点D1的坐标_________,点D旋转到点D1所经过的路线长__________;
(2)请你在△ACD的三个内角中任选二个锐角,若你所选的锐角是________,则它所对应的正弦函数值是_________;
(3)将四边形A1B1C1D1平移,得到四边形A2B2C2D2,若点D2 (4,5),画出平移后的图形.(友情提示:画图时请不要涂错阴影的位置哦!)