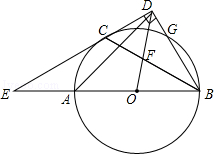
如图, AB为⊙ O的直径, C, G是⊙ O上两点,过点 C的直线 CD⊥ BG于点 D,交 BA的延长线于点 E,连接 BC,交 OD于点 F,且 BC平分∠ ABD.
(1)求证: CD是⊙ O的切线;
(2)若 ,求∠ E的度数;
(3)连结 AD,在(2)的条件下,若 CD=2 ,求 AD的长.
相关知识点
推荐套卷
如图, AB为⊙ O的直径, C, G是⊙ O上两点,过点 C的直线 CD⊥ BG于点 D,交 BA的延长线于点 E,连接 BC,交 OD于点 F,且 BC平分∠ ABD.
(1)求证: CD是⊙ O的切线;
(2)若 ,求∠ E的度数;
(3)连结 AD,在(2)的条件下,若 CD=2 ,求 AD的长.
