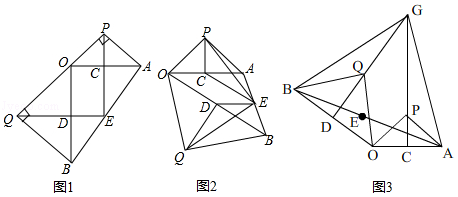
△ OPA和△ OQB分别是以 OP、 OQ为直角边的等腰直角三角形，点 C、 D、 E分别是 OA、 OB、 AB的中点．
（1）当∠ AOB＝90°时如图1，连接 PE、 QE，直接写出 EP与 EQ的大小关系；
（2）将△ OQB绕点 O逆时针方向旋转，当∠ AOB是锐角时如图2，（1）中的结论是否成立？若成立，请给出证明；若不成立，请加以说明．
（3）仍将△ OQB绕点 O旋转，当∠ AOB为钝角时，延长 PC、 QD交于点 G，使△ ABG为等边三角形如图3，求∠ AOB的度数．
相关试题
如图，墙壁上的展品最高点与地面的距离PF=3．2 m，最低点与地面的距离QF ="2" m，观赏者的眼睛E 距地面1．6 m．经验表明，当水平视线EH 与过P、Q、E 三点的圆相切于点E 时，视角最大，站在此处观赏最理想．求此时点E 到墙壁的距离EH．
如图，AB 是半圆O 的直径，AD 和BC 是它的两条切线，切点分别为A、B，CO 平分∠BCD．
（1）求证：CD是半圆O的切线；
（2）若AC=2，BD=3，求AB的长．．
相关知识点
推荐套卷
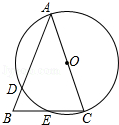
粤公网安备 44130202000953号