为了深化课程改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“国际象棋”、“音乐舞蹈”和“书法”等多个社团,要求每位学生都自主选择其中一个社团,为此,随机调查了本校部分学生选择社团的意向.并将调查结果绘制成如下统计图表(不完整):
选择意向 |
文学鉴赏 |
国际象棋 |
音乐舞蹈 |
书法 |
其他 |
所占百分比 |
a |
20% |
b |
10% |
5% |
根据统计图表的信息,解答下列问题:
(1)求本次抽样调查的学生总人数及a、b的值;
(2)将条形统计图补充完整;
(3)若该校共有1300名学生,试估计全校选择“音乐舞蹈”社团的学生人数.

推荐套卷
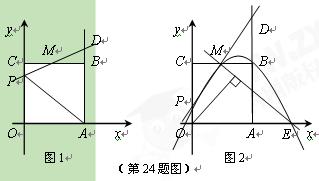
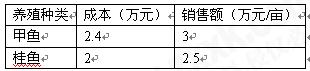
 收益多少万元?(收益=销售额-成本)
收益多少万元?(收益=销售额-成本)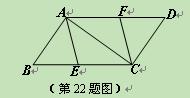
 )。
)。

 粤公网安备 44130202000953号
粤公网安备 44130202000953号