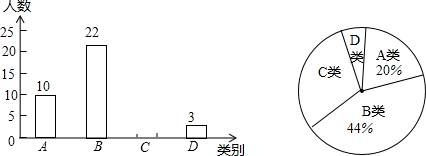
某校为了解本校九年级男生“引体向上”项目的训练情况，随机抽取该年级部分男生进行了一次测试（满分15分，成绩均记为整数分），并按测试成绩m（单位：分）分成四类：A类（12≤m≤15），B类（9≤m≤11），C类（6≤m≤8），D类（m≤5）绘制出以下两幅不完整的统计图，请根据图中信息解答下列问题：
（1）本次抽取样本容量为 ，扇形统计图中A类所对的圆心角是 度；
（2）请补全统计图；
（3）若该校九年级男生有300名，请估计该校九年级男生“引体向上”项目成绩为C类的有多少名？
相关试题
试解答下列问题：（2+2+4+2=10分）
(1)在图1我们称之为“8字形”，请直接写出∠A，∠B，∠C，∠D之间的数量关系：；
(2)仔细观察，在图2中“8字形”的个数是个；
(3)在图2中，若∠D=40°，∠B=36°，∠DAB和∠BCD的平分线AP和CP相交于点P，并且与CD、AB分别相交于M、N．试求∠P的度数；
(4)如果图2中∠D和∠B为任意角时，其他条件不变，试写出∠B与∠P、∠D之间数量关系．
（本题6分）在正方形网格中，每个小正方形的边长均为1个单位长度，△ABC三个顶点的位置如图所示，现将 △ABC平移，使点A移动到点A′，点B′，点C′分别是B、C的对应点．
(1)请画出平移后的△A′B′C′；
(2)△A′B′C′的面积是 ；
(3)若连接AA′、CC′，则这两条线段之间的关系是________ ______．
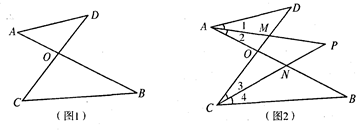
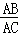=a，点G，H分别在边AB，DC上，且HA=HG，点E为AB边上的一个动点，连接HE，把△AHE沿直线HE翻折得到△FHE．如图1，当DH=DA时，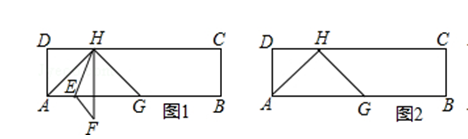
相关知识点
推荐套卷
粤公网安备 44130202000953号