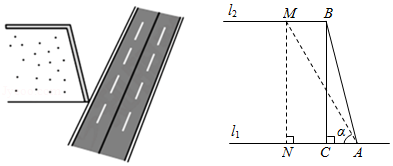
某高速公路管理部门工作人员在对某段高速公路进行安全巡检过程中

更新 2022-09-04
科目数学
题型解答题
难度中等
浏览 219

某高速公路管理部门工作人员在对某段高速公路进行安全巡检过程中，发现该高速公路旁的一斜坡存在落石隐患．该斜坡横断面示意图如图所示，水平线 $l_{1} / / l_{2}$ ，点 $A$ 、 $B$ 分别在 $l_{1}$ 、 $l_{2}$ 上，斜坡 $AB$ 的长为18米，过点 $B$ 作 $BC ⊥ l_{1}$ 于点 $C$ ，且线段 $AC$ 的长为 $2 \sqrt{6}$ 米．

（1）求该斜坡的坡高 $BC$ ；（结果用最简根式表示）

（2）为降低落石风险，该管理部门计划对该斜坡进行改造，改造后的斜坡坡角 $α$ 为 $60 °$ ，过点 $M$ 作 $MN ⊥ l_{1}$ 于点 $N$ ，求改造后的斜坡长度比改造前的斜坡长度增加了多少米？

登录免费查看答案和解析

相关试题

如图,小丽在观察某建筑物．

（1）请你根据小亮在阳光下的投影,画出建筑物在阳光下的投影．
（2）已知小丽的身高为,在同一时刻测得小丽和建筑物的投影长分别为和,求建筑物的高．

题型：未知
难度：未知

收藏答案/解析

如图,CD,EF表示高度不同的两座建筑物,已知CD高15米,小明站在A处,视线越过CD,能看到它后面的建筑物的顶端E,此时小明的视角∠FAE=45°,为了能看到建筑物EF上点M的位置,小明延直线FA由点A移动到点N的位置,此时小明的视角∠FNM=30°,求AN之间的距离．

题型：未知
难度：未知

收藏答案/解析

为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担．李明按照相关政策投资销售本市生产的一种新型节能灯．已知这种节能灯的成本价为每件元,出厂价为每件元,每月销售量（件）与销售单价（元）之间的关系近似满足一次函数: ．
（1）李明在开始创业的第一个月将销售单价定为元,那么政府这个月为他承担的总差价为多少元?
（2）设李明获得的利润为（元）,当销售单价定为多少元时,每月可获得最大利润?
（3）物价部门规定,这种节能灯的销售单价不得高于元．如果李明想要每月获得的利润不低于元,那么政府为他承担的总差价最少为多少元?