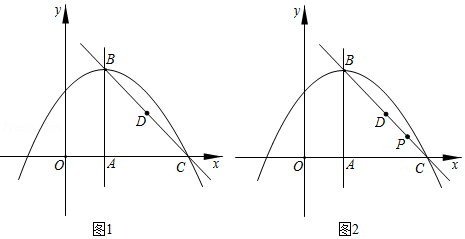
如图1,抛物线 经过点 ,顶点为 ,对称轴 与 轴相交于点 , 为线段 的中点.
(1)求抛物线的解析式;
(2) 为线段 上任意一点, 为 轴上一动点,连接 ,以点 为中心,将 逆时针旋转 ,记点 的对应点为 ,点 的对应点为 .当直线 与抛物线 只有一个交点时,求点 的坐标.
(3) 在(2)的旋转变换下,若 (如图 .
①求证: .
②当点 在(1)所求的抛物线上时,求线段 的长.
推荐套卷
如图1,抛物线 经过点 ,顶点为 ,对称轴 与 轴相交于点 , 为线段 的中点.

(1)求抛物线的解析式;
(2) 为线段 上任意一点, 为 轴上一动点,连接 ,以点 为中心,将 逆时针旋转 ,记点 的对应点为 ,点 的对应点为 .当直线 与抛物线 只有一个交点时,求点 的坐标.
(3) 在(2)的旋转变换下,若 (如图 .
①求证: .
②当点 在(1)所求的抛物线上时,求线段 的长.