某校足球队需购买 、 两种品牌的足球.已知 品牌足球的单价比 品牌足球的单价高20元,且用900元购买 品牌足球的数量用720元购买 品牌足球的数量相等.
(1)求 、 两种品牌足球的单价;
(2)若足球队计划购买 、 两种品牌的足球共90个,且 品牌足球的数量不小于 品牌足球数量的2倍,购买两种品牌足球的总费用不超过8500元.设购买 品牌足球 个,总费用为 元,则该队共有几种购买方案?采用哪一种购买方案可使总费用最低?最低费用是多少元?
相关知识点
推荐套卷
 和
和 是绕点
是绕点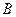 旋转的两个相似三角形,其中
旋转的两个相似三角形,其中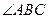 与
与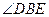 、
、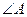 与
与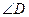 为对应角.
为对应角.
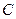 、
、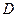 在同一条直线上的位置时,请直接写出线段
在同一条直线上的位置时,请直接写出线段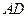 与线段
与线段 的关系;
的关系;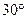 角的直角三角形,且两个三角形旋转到如图2的位置时,试确定线段
角的直角三角形,且两个三角形旋转到如图2的位置时,试确定线段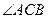 =
= ,
,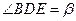 ,在绕点
,在绕点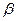 的式子表示夹角的度数;若改变,请说明理由.
的式子表示夹角的度数;若改变,请说明理由. 中,二次函数
中,二次函数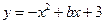 的图象经过点
的图象经过点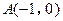 ,顶点为
,顶点为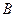 .
.
 的坐标为
的坐标为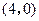 ,连接
,连接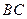 ,过点
,过点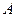 作
作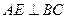 ,垂足为点
,垂足为点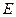 .当点
.当点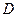 在直线
在直线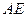 上,且满足
上,且满足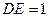 时,求点
时,求点 中,
中, 的外接圆与
的外接圆与 轴交于点
轴交于点 ,
, ,
, 求
求 的长.
的长.
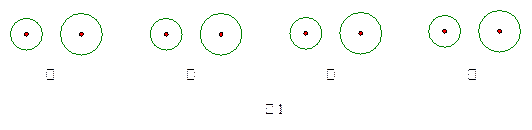
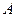 、
、 在直线MN上,AB=11厘米,
在直线MN上,AB=11厘米, 、
、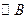 的半径均为1厘米.
的半径均为1厘米. 也不断增大,其半径
也不断增大,其半径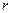 (厘米)与时间t(秒)之间的关系式为
(厘米)与时间t(秒)之间的关系式为 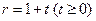 .请直接写出点
.请直接写出点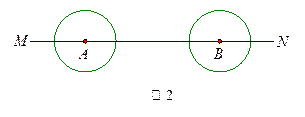
 中,
中, 、
、 两点在
两点在 轴的上方,点
轴的上方,点 的坐标是(-1,0).以点
的坐标是(-1,0).以点 ,并把
,并把 的横坐标是2,求点
的横坐标是2,求点

 粤公网安备 44130202000953号
粤公网安备 44130202000953号